Compact WHO growth standard

library(centile)

Background

The WHO Growth Standards are published in the form of reference tables. The age grid and the numeric formatting in these tables is somewhat detailed. For example the height, BMI and weight references have 2026 age points, head circumference has 1857 age points and the weight-for-height references are stored in a table with 551 height points.

The tables may contain more detail than needed, potentially wasting resources and slowing down computing in time-critical applications. This section looks into the question whether we can reduce the number of rows in these tables without affecting precision of the calculations.

Let us study the height references for boys.

full <- load_reference("who_2006_hgt_male_", pkg = "centile")
head(full)
#> # A tibble: 6 × 4
#>        x     L     M      S
#>    <dbl> <dbl> <dbl>  <dbl>
#> 1 0          1  49.9 0.0380
#> 2 0.0027     1  50.1 0.0378
#> 3 0.0055     1  50.2 0.0378
#> 4 0.0082     1  50.4 0.0376
#> 5 0.011      1  50.6 0.0375
#> 6 0.0137     1  50.8 0.0374
tail(full)
#> # A tibble: 6 × 4
#>       x     L     M      S
#>   <dbl> <dbl> <dbl>  <dbl>
#> 1  18.7     1  176. 0.0417
#> 2  18.8     1  176. 0.0416
#> 3  18.8     1  176. 0.0415
#> 4  18.9     1  177. 0.0414
#> 5  19       1  177. 0.0413
#> 6  19.1     1  177. 0.0413
nrow(full)
#> [1] 2026

g <- make_agegrid("compact")
head(g)
#> [1] 0.0000 0.0027 0.0055 0.0082 0.0110 0.0137
tail(g)
#> [1] 18.5 19.0 19.5 20.0 20.5 21.0
length(g)
#> [1] 95

The make_agegrid() function creates an age grid that fairly detailed for the early ages, but less so for later ages. Can we reduce 2026 into 95 rows? We use linear interpolation to reduce the reference to 95 rows, as follows:

L <- approx(y = full$L, x = full$x, xout = g)$y
M <- approx(y = full$M, x = full$x, xout = g)$y
S <- approx(y = full$S, x = full$x, xout = g)$y
cpt <- data.frame(x = g, L = L, M = M, S = S)
attr(cpt, "study") <- attr(full, "study")
is_reference(cpt)
#> [1] TRUE

Now let calculate fictitious measurements using both references, and compare the results:

grid <- expand.grid(z = -2:2, x = seq(0, 19, 0.01))
grid$yf <- z2y(x = grid$x, z = grid$z, ref = full)
grid$yc <- z2y(x = grid$x, z = grid$z, ref = cpt)
with(grid, plot(x = x, y = yf - yc, type = "l"))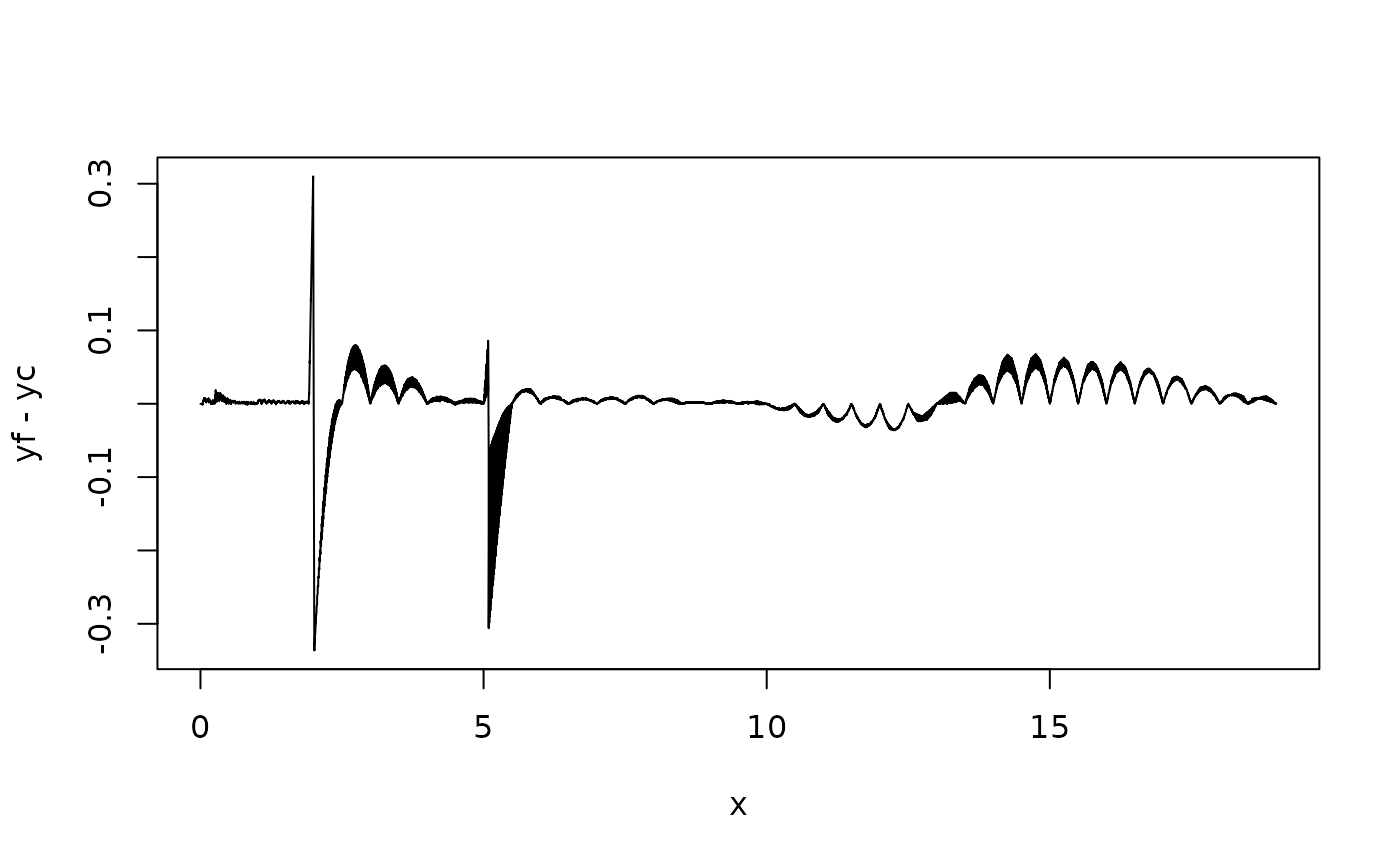

The figure shows that the reculculate heights hoover around zero, as expected. Correspondence in the first two years is very good. The age 2 and 5 years are points at which different references have been combined. Age those ages the difference can be up to 3mm. It would be desirable if all differences would be within a range of, say, 1 mm. In order to achieve this, we need to more dense age grid.

Stef van Buuren

Background